Paul Beale
Professor of Physics
Department of Physics
University of Colorado Boulder
R. K. Pathria and Paul D. Beale, Statistical Mechanics
Third Edition (Academic, Boston, 2011)
This new edition of Raj
Pathria's classic graduate statistical mechanics textbook includes new sections
on Bose-Einstein condensation and degenerate Fermi behavior of ultracold atomic
gases, and two new chapters on computer simulations and thermodynamics of the
early universe. The authors have also added new sections on chemical and phase
equilibrium, and expanded their discussions of correlations and scattering, quantized
fields, finite-size effects, and the fluctuation-dissipation theorem. We hope
this new edition will continue to provide new generations of students with
solid training in the methods of statistical physics. The web page for the book
can be found at
http://www.elsevierdirect.com/product.jsp?isbn=9780123821881
or by going the Elsevier web site
http://elsevierdirect.com
and searching for Pathria or Beale.
Associated Mathematica
files for solving the two-dimensional Ising model on a finite square lattice can
be found on the Companion site.
Here is the direct link.
The corrections to the first printing can also be
found in the errata file on the
Companion site. The most up-to-date corrections are posted in the
errata file on this site.
These corrrections to the text will made in the second printing.
Course instructors who
have been issued login information from the publisher can download a solutions manual
by clicking
Manual.
Here is a direct link to the instructor login page.
Link to a University of Colorado Boulder promotional video.
Link to an episode of Stan Lee's Superhumans on The History Channel featuring Darren Taylor, a.k.a. Professor Splash, who can dive off a 10 meter platform into a kiddie pool with 12 inches of water. I provide the physics analysis.
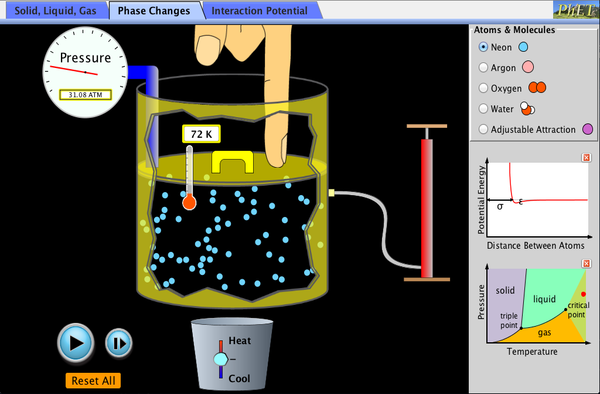
Try the States
of Matter Java Applet on the Physics Education Technology Web site:
Explore the solid, liquid and vapor phases of neon, argon, oxygen and water.
The PhET simulation was based on molecular dynamics code I developed long ago.
Paul D. Beale
Professor of Physics
Department of Physics
E1B32 Duane Physics, 390 UCB
University of Colorado at Boulder
Boulder, CO 80309-0390
(303) 492-1685
(303) 492-3352 (FAX)
(303) 241-3308 (cell)
Paul.Beale@Colorado.edu
Home Page:
http://spot.colorado.edu/~beale
B.S. Physics,
University of North Carolina, Chapel Hill (1977)
Ph.D. Physics Cornell University, 1982.
Professor of Physics, University of Colorado at Boulder (1997-)
Associate Professor of Physics, University of Colorado at Boulder (1991-1997)
Assistant Professor of Physics, University of Colorado at Boulder (1984-1991)
Postdoctoral Research Associate, Department of Theoretical Physics, Oxford
University (1982-1984).
Administrative Positions
Faculty Associate for Curricular Affairs, College of Arts and Sciences
(1994-1996)
Acting Chair of the Department of Fine Arts (1996)
Dean of Summer School (1996)
Associate Dean for Faculty Affairs, College of Arts and Sciences (1996)
Associate Dean for the Natural Sciences, College of Arts and Sciences
(1997-1999)
Director of the Condensed Matter Laboratory, Department of Physics (1999-2001)
Acting Associate Dean for the Social Sciences, College of Arts and Sciences
(2000)
Acting Associate Dean for the Natural Sciences, College of Arts and Sciences
(2000)
Director of the Honors Program (2006-2008)
Chair of the Department of Physics
(2008-present)
My general field of research is the thermodynamics and statistical mechanics of
condensed matter systems. This includes theoretical studies related to critical
phenomena and phase transitions, ferroelectrics, Landau theories, hysteresis in
spin models, magnetic materials, failure modes in random materials, theories of
melting, effects of noise on nonlinear dynamical systems, phenomenological
finite-size scaling, Monte Carlo methods, commensurate-incommensurate
transitions, renormalization-group methods, and structural phase transitions.
My recent work includes a calculation of the exact distribution of energies in
the two-dimensional Ising model. By using Kauffman's generalization of Onsager's
solution of the two-dimensional Ising model, one can calculate the exact form
of the partition function in the form of a low-temperature series expansion.
Since the coefficients of the low-temperature series give the number of
different states with a given energy, one can use the coefficients to calculate
the exact distribution of energies at any specified temperature. This solution
provides an exact distribution that can be used to verify the accuracy and
convergence of Monte Carlo simulations.
I have recently developed new class of pseudorandom number generators based on Pohlig-Hellman exponentiation ciphers. The method generates uniform pseudorandom streams by encrypting simple sequences of short integer messages into ciphertexts by exponentiation modulo prime numbers. The advantages of the method are: the method is trivially parallelizable by parameterization with each pseudorandom number generator derived from an independent prime modulus, the method is fully scalable on massively parallel computing clusters due to the large number of primes available for each implementation, the seeding and initialization of the independent streams is simple, the method requires only a few integer multiply-mod operations per pseudorandom number, the state of each instance is defined by only a few integer values, the period of each instance is different, and the method passes a battery of intrastream and interstream correlation tests using up to 1013 pseudo- random numbers per test. We propose an implementation using 32-bit prime moduli with small exponents that require only a few 64-bit multiply-mod operations that can be executed directly in hardware. The 32-bit implementation we propose has millions of possible instances, all with periods greater than 1018. A 64-bit implementation depends on 128-bit arithmetic, but has more than 1015 possible instances and periods greater than 1037.
See http://arxiv.org/abs/1411.2484 and
http://spot.colorado.edu/~beale/Pohlig-Hellman.
Selected Publications:
"A new class of scalable parallel pseudorandom number generators based on Pohlig-Hellman exponentiation ciphers,"
Paul D. Beale, http://arxiv.org/abs/1411.2484 (2014).
"Microscopic origins of first-order Sm-A–Sm-C phase behavior in de Vries smectic
liquid crystals,"
Zachary V. Kost-Smith, Paul D. Beale, Noel A. Clark, and Matthew A. Glaser,
Physical Review E 87, 050502(R)-050507(R) (2013).
"A Thoughtful Approach to Instruction: Course transformation for the rest of us,"
Stephanie V. Chasteen, Katherine K. Perkins, Paul D. Beale, Steven J. Pollock, Carl E. Wieman,
Journal of College Science Teaching, vol. 40, no. 4, 24-30 (2011).
"Transforming Upper-Division Quantum Mechanics: Learning Goals and Their Assessment,"
Steven Goldhaber, Steven J. Pollock, Michael Dubson, Paul D. Beale and Katherine K. Perkins,
Proceedings of the Physics Education Research Conference,
AIP Conference Proceedings Volume 1179,
Eds: Mel Sabella, Charles Henderson, Chandralekha Singh (2009)
"Grain boundary free energy of hard disk assemblies under constant volume
via thermodynamic integration," Mark T. Lusk, Michael R. Fellinger and
Paul D. Beale, Journal of Chemical Physics, 124 064707-064716 (2006).
"Grain Boundary Free Energy in an Assembly of Elastic Disks", Mark T.
Lusk and Paul D. Beale, Physical Review E, 69, 026117 (2004).
"Three-Dimensional Hard Dumbbell Solid Free Energy Calculation Via the
Fluctuating Cell Model", Steven A. Kadlec, Paul D. Beale and James Rainwater,
Proceedings of the Fifteenth Symposium on Thermophysical Properties, published
in the International Journal of Thermophysics, 25 1415 (2004).
"Acoustic Crystal Thermodynamic Integration Method", Paul D Beale,
Physical Review E 66, 036132-036139 (2002).
"Two Dimensional Hard Dumbbells,: I. Flucutating Cell Model", S. C.
Gay, J. C. Rainwater, P.D. Beale, Journal of Chemical Physics, 112,
9841-9848 (2000).
"Thermodynamic perturbation theory applied to the dipolar heteronuclear
dumbell fluid", S.C. Gay, P.D. Beale and J.C. Rainwater, Mol. Phys., 96,
301 (1999).
"Solid-liquid equilibrium of dipolar heteronuclear dumbells in a
generalized van der Walls theory: Application to methyl chloride", S.C.
Gay, P.D. Beale and J.C. Rainwater, J. Chem. Phys., 109, 6820 (1998).
"Exact Distribution of Energies in the Two-Dimensional Ising Model",
Paul D. Beale, Physical Review Letters 76, 78-81 (1996). You can
download a Mathematica routine that will calculate the exact partition function
for the two dimensional Ising model on an nxm lattice. The program determines
the coefficients of the low temperature power series expansion. IsingExactMathematica.html
"Breakdown of Two-Phase Random Resistor Networks," P.M. Duxbury, P.D.
Beale, Phys. Rev. B 51, 476 (1995).
"Comparison of Classical Nucleation Theories with Monte Carlo Simulations
of Ising Models," Paul D. Beale, Integrated Ferroelectrics 4,
107-111 (1994).
"Dielectric Breakdown in Continuous Models of Metal-Loaded Dielectrics,"
Mark F. Gyure, Paul D. Beale, Phys. Rev. B 46, 3736-3746 (1992).
"Grain-size effects in ferroelectric switching," H.M. Duiker, P.D.
Beale, Phys. Rev. B 41, 490-495 (1990).
"Noise-induced escape from attractors in one-dimensional maps," P.D.
Beale, Phys. Rev. A 40, 3998-4003 (1989).
"Elastic fracture in random materials," P.D. Beale and D.J.
Srolovitz, Physical Review B. 37, 5500-5507 (1988).
"Dielectric breakdown in metal-loaded dielectrics," P.D. Beale and
P.M. Duxbury, Physical Review B. 37, 2785-2791 (1988).
"The breakdown properties of quenched random systems - the random fuse
network," P.M. Duxbury, P.L. Leath and P.D. Beale, Physical Review B 36,
367-380 (1987).
"Size effects of breakdown in quenched random media," P.M. Duxbury,
P.D. Beale and P.L. Leath, Physical Review Letters 57, 1052 (1986).
"Finite-size scaling of the two-dimensional axial next-nearest neighbor
Ising model," P.D. Beale, P.M. Duxbury and J.M. Yeomans, Physical Review B
31, 7166 (1985).
"Finite-size scaling at an Ising tricritical point," P.D. Beale,
Journal of Physics A 17, L335 (1984).
"Wavevector scaling and the phase diagram of the chiral clock model,"
P.M. Duxbury, J. Yeomans and P.D. Beale, Journal of Physics A 17, L179 (1984).
"Renormalization-group study of crossover in structural phase
transitions," P.D. Beale, S. Sarker and J.A. Krumhansl,Physical Review B
24 , 266 (1981).
My recent bicycle rides
Check out my daughter Melanie's collegiate and Pro cycling results.
Interested in flying? Have a look at my
Beechcraft Bonanza.
Return to the Department of Physics
Home Page