Generation of traveling solitons in one-dimensional monatomic quartic lattices

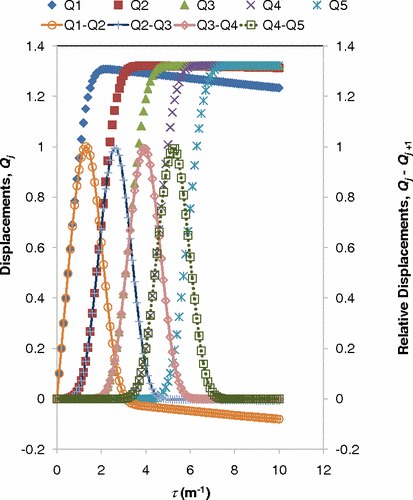
Generation of traveling soliton waves on a one-dimensional monatomic quartic lattice is investigated using numerical techniques. Solitons are generated by the application of an external forcing function to the end atom of a free chain of monatomic atoms. Multiple traveling solitons are observed to flow down the chain when the strength of the forcing function, applied over a period of time, is beyond a threshold value. Total number of traveling solitons in the chain increases rapidly as the strength of the forcing function is increased beyond this critical value. The amplitudes and velocities of these multiple solitons saturate with the increasing strength of the forcing function. The frequencies and wave vectors of all the traveling solitons on the quartic lattice are independent of forcing functions and lie within a narrow range of values. These results are compared with those for solitons on a one-dimensional monatomic Toda lattice generated using similar forcing functions.